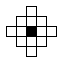 Schematic of the neighbourhoods used in the texture synthesis algorithm
Schematic of the neighbourhoods used in the texture synthesis algorithmFast Version on a Gaussian Pyramid with K Nearest Search
This algorithm has been recently published in IEEE Transactions on Pattern Analysis and Machine Intelligence 2004. The algorithm is based on the theory that an MRF with a much stronger conditional independence criteria, can be decomposed into its marginal distributions defined on its cliques. This stronger conditional independence criteria actually defines this strong-MRF on a triangulated graph. From graph theory [Judea Pearl "Probabilistic Reasoning in Intelligent Systems", 1988] and ANOVA log-linear construction [Bishop et al "Discrete Multivariate Analysis: Theory and Practice", 1975] it can be shown that this model can have its auto-model defined as combination of the marginal distributions defined on the pairwise cliques. I use this directly calculable auto-model to synthesis a variety of VisTex textures as presented on this webpage.
In the presented paper, I advocate using a Parzen density estimation of the pairwise marginal distributions with only a box kernel and a smoothing parameter equal to 0. This is possible using Ashikhmin's argument as presented in Synthesizing Natural Textures. Although this dramatically reduces the stochastic nature inherent in the model, it does allow to show that quite a variety of textures can be modelled with just second order statistics. This gives credence for using second order models for classification.
The model is not perfect. It is restrained by the assumptions made by the theory on the texture, and in the current implementation the Parzen density estimation of the pairwise marginal distributions does not take into account the stochastic nature of texture. The Parzen density estimation of the pairwise marginal distributions needs to be estimated with respect to entropy as in Zhu, Wu and Mumford's minimax entropy model ["FRAME: filters, random fields, and minimax entropy towards a unified theory for texture modeling", Proceedings 1996 IEEE Computer Society Conference on Computer Vision and Pattern Recognition].
In the synthesis results presented here, I have experimented with different Parzen smoothing (ie window) parameters. For an input parameter of window, I find a window size that equals the average distance to the first k nearest neighbours, where
k = ImageSize^(4/7)*window/100
This value of k is from on Silverman ["Density estimation for statistics and data analysis", 1986] who says on page 99, that; "In the case of the generalized nearest neighour method .... the ideal k .... would be proportional to ImageSize^(4/(d+4)." As the data is of RGB pixels, I have used the value of k as given above.
The synthesis algorithm employed is based on my earlier algorithm for nonparametric MRF texture synthesis. It is a multiscale algorithm, meaning that ImageSize is dependent on scale. Calculating k at each scale gives a small window size at low resolution with increasing window size at each higher resolution. This fits neatly in with De Bonet's work ["Multiresolution sampling procedure for analysis and synthesis of texture images", SIGGRAPH: Computer Graphics, 1997] who employed a threshold that allowed the "variability" to increase with each higher resolution.
| Download Source Code | Copyright (C) 2002, by Rupert Paget, all rights reserved. |
The source code requires ImageMagick to be preinstalled. To compile the code, run gmake in the parent directory. There are two makefiles, one in parent directory, and in the src directory. If the code does not compile, both makefiles will need to be edited. I have written one for a sun (default) and one for an sgi machine, but I give no guarantees that they will work.
nonparaMRF_strong [-l levels] [-n neighOrder] [-s] [-t treeMax] [-i iterations] [-w window] [-c] [-x cols] [-y rows] [-m maskfile] [-h] texturefile
where
Default values are : levels = 256, neighOrder = 1, square = false, treeMax = 6, iterations = 1, window = 0, cyclic = false
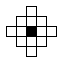 Schematic of the neighbourhoods used in the texture synthesis algorithm
Schematic of the neighbourhoods used in the texture synthesis algorithmThese times were compiled on a distributed system of mainly SunBlades 100: 500 MHz, 256 MBytes RAM. The input textures were 128x128 pixel images, and the output synthesised textures were 256x256 pixel images. The run times are basically dependent on output image size and the type of input texture. This is due to the search algorithm used in the code. If the input texture is fairly uniform in colour, then the search algorithm will be more of an exhaustive search, and therefore more dependent on input image size. Time stamps are in "Days Hours:Minutes:Seconds".
| Neighbourhood | Iterations | Window | # of Tests | Fastest Run Time | Slowest Run Time | Mean Run Time | Stdev Run Time |
|---|---|---|---|---|---|---|---|
| 1 -s | 2 | 0 | 165 | 0 00:20:36 | 0 02:23:26 | 0 00:49:51 | 0 00:52:52 |
| 1 -s | 2 | 1 | 165 | 0 00:20:17 | 0 02:15:57 | 0 00:52:04 | 0 00:56:14 |
| 1 -s | 2 | 2 | 165 | 0 00:20:40 | 0 02:05:29 | 0 00:54:30 | 0 00:57:33 |
| 1 -s | 2 | 5 | 165 | 0 00:21:03 | 0 02:21:00 | 0 01:00:27 | 0 01:03:45 |
| 1 -s | 2 | 10 | 165 | 0 00:22:19 | 0 03:23:51 | 0 01:13:16 | 0 01:18:38 |
| 1 -s | 2 | 20 | 165 | 0 00:42:51 | 0 03:11:26 | 0 01:38:57 | 0 01:44:30 |
| 2 -s | 2 | 0 | 165 | 0 00:42:04 | 0 03:33:01 | 0 01:47:50 | 0 01:53:34 |
| 2 -s | 2 | 1 | 165 | 0 00:43:51 | 0 03:46:01 | 0 01:51:06 | 0 01:57:23 |
| 2 -s | 2 | 2 | 165 | 0 00:44:22 | 0 03:56:17 | 0 01:54:03 | 0 02:00:32 |
| 2 -s | 2 | 5 | 165 | 0 00:42:26 | 0 06:25:51 | 0 02:08:10 | 0 02:16:58 |
| 2 -s | 2 | 10 | 165 | 0 00:45:59 | 0 05:52:28 | 0 02:24:34 | 0 02:32:38 |
| 2 -s | 2 | 20 | 165 | 0 01:13:37 | 0 06:09:12 | 0 03:08:43 | 0 03:19:42 |
| 3 -s | 2 | 0 | 165 | 0 01:15:27 | 0 09:23:11 | 0 03:21:46 | 0 03:37:40 |
| 3 -s | 2 | 1 | 165 | 0 01:15:12 | 0 11:34:16 | 0 03:26:13 | 0 03:44:36 |
| 3 -s | 2 | 2 | 165 | 0 01:15:46 | 0 10:24:21 | 0 03:34:17 | 0 03:48:51 |
| 3 -s | 2 | 5 | 165 | 0 01:15:20 | 0 10:57:20 | 0 03:50:02 | 0 04:06:04 |
| 3 -s | 2 | 10 | 165 | 0 01:19:03 | 0 13:59:07 | 0 04:24:19 | 0 04:28:46 |
| 3 -s | 2 | 20 | 165 | 0 02:00:27 | 0 18:26:09 | 0 05:12:29 | 0 05:21:11 |
| 4 -s | 2 | 0 | 165 | 0 01:54:34 | 0 12:39:00 | 0 05:14:56 | 0 05:35:18 |
| 4 -s | 2 | 1 | 165 | 0 02:02:48 | 0 11:51:39 | 0 05:18:49 | 0 05:41:03 |
| 4 -s | 2 | 2 | 165 | 0 01:53:47 | 0 15:37:25 | 0 05:33:14 | 0 05:36:28 |
| 4 -s | 2 | 5 | 165 | 0 02:05:52 | 0 14:46:07 | 0 06:00:18 | 0 05:54:53 |
| 4 -s | 2 | 10 | 165 | 0 02:10:48 | 0 12:57:24 | 0 06:38:43 | 0 06:52:57 |
| 4 -s | 2 | 20 | 165 | 0 02:50:30 | 0 18:18:05 | 0 07:38:30 | 0 07:22:53 |
Email Rupert Paget at: dr@rupertpaget.com
This site was proofread by
English Editing Experts.